ある曲面S上で定義されるスカラー場Fに対し、
をFのS上での面積分といいます。
ここで、
dS
はS上の微小面積素です。
曲面Sが閉曲面の場合、
と書きます。
ベクトル場
F
を考えます。
曲面Sの単位法線ベクトルを
n
とすると
F・n
はスカラー場となります。
これをFとおいて面積分すると、
となります。
ここで、
dS = ndS
とおくと上の式は
となります。
この
dS
を面積素ベクトルといいます。
物理学ではこのように曲面を貫くベクトル場の法線方向成分のみが問題となる場合が多いので、
∫F・dS
という形の式を、
単にベクトル場
F
の曲面S上での面積分ということもあります。
曲面S上の点
r
は媒介変数を持ちいて
r(u,v)=(
x(u,v), y(u,v), z(u,v)
)
と言う風に表されます。ここで、uがごく小さい値
du
だけ変化したとき、
r
は
だけ変化します。同様にvが
dv
だけ変化したとき、
r
は
だけ変化します。
このとき、
du
および
dv
はSの接ベクトルになっています。
図1のように
du
および
dv
はSと
dS, n
の間には
という関係があります。よって
dS
は、
となります。
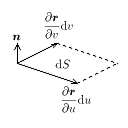 dS と du, dv の関係
dS と du, dv の関係
ここで
×
を座標成分ごとにあらわすと
となることと、
であることから、結局
dS
は
dS = (
dydz,dzdx,dxdy
)
と表すことができます。
よって、
F=(
Fx,Fy,Fz
)
とおくと、
線積分は
∫
F・dS = ∫∫(
Fxdydz+Fydzdx+Fzdxdy
)
となります。

