ヤコビの楕円関数
第1種不完全楕円積分 F(φ, k) の逆関数として定義される楕円関数群をヤコビの楕円関数(Jacobian elliptic functions)と呼びます。
-
φ(u, k) = F-1(φ, k)このφを(ヤコビの楕円関数の)振幅(amplitude)と呼ぶ。
-
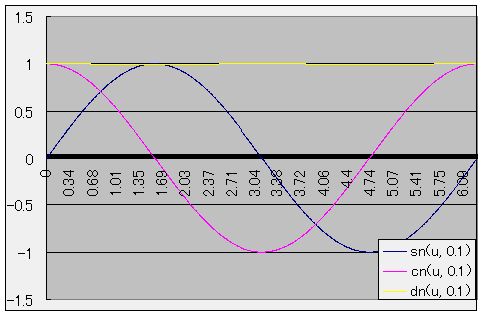
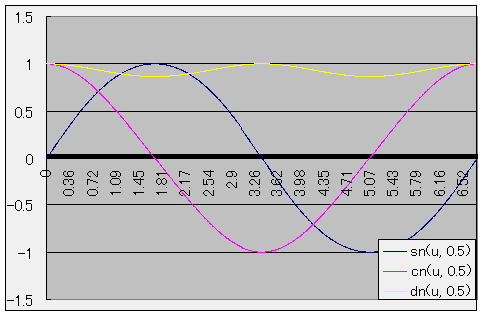
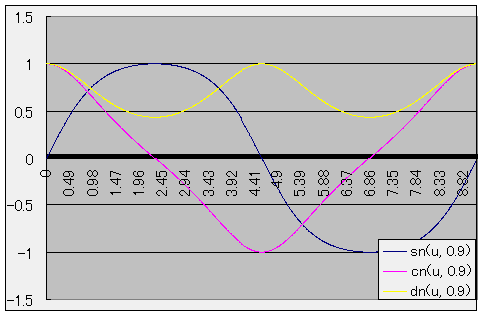
sn(u, k) = sin(φ)
-
cn(u, k) = cos(φ)
-
dn(u, k) = √(1 - k2sn2(u, k))
執筆予定
ヤコビの楕円関数の公式 θ(テータ)関数 テータ関数とヤコビの楕円関数との関係
メモ
諸定数
k … ヤコビの楕円関数の率(modulus、複数形 moduli。母数、法と訳す場合も)。 k' … 補率(complementary modulus)。k' = √(1 - k^2) 数値計算ライブラリなどでは、 m = k^2, m' = k'^2 = 1 - m というように、 率・補率の2乗をパラメータとして使う場合も多い。 (k は公式中のほとんどの箇所で、k^2 の形で出てくるため、 m = k^2 を使った方が計算効率がいい。) K = K(k) … 率 k の完全楕円積分。ヤコビの楕円関数の周期の1つになる。 K' = K(k') … 率 k' の完全楕円積分。これもヤコビの楕円関数の周期の1つになる。 Legendre は k = sinα k' = cosα となるような値αを定義し、率角(modular angle)と呼んだ。
グラフ
簡単な性質
sn(-u) = -sn(u) sn(2K - u) = sn(u) cn(-u) = cn(u) sn^2 + cn^2 = 1 k^2 sn^2 + dn^2 = 1 dn^2 - k^2 cn^2 = k'^2
周期
sn(u + 2mK + 2niK', k) = (-1)^m sn(u, k) cn(u + 2mK + 2niK', k) = (-1)^(m+n) cn(u, k) dn(u + 2mK + 2niK', k) = (-1)^n dn(u, k)
| 周期 | 零点 | 極 | |
|---|---|---|---|
| sn | 4K, 2i K' | 2mK + 2n i K' | 2m K + (2n+1) i K' |
| cn | 4K, 2(K + iK') | (2m+1)K + 2n i K' | 2m K + (2n+1) i K' |
| dn | 2K, 4i K' | (2m+1)K + (2n+1) i K' | 2m K + (2n+1) i K' |
| Im(u)\Re(u) | 0 | K | 2K | 3K |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | -1 |
| 1 | 0 | -1 | 0 | |
| 1 | k' | 1 | k' | |
| K' | ∞ | 1/k | ∞ | -1/k |
| ∞ | -ik'/k | ∞ | ik'/k | |
| ∞ | 0 | ∞ | 0 | |
| 2K' | 0 | 1 | 0 | -1 |
| -1 | 0 | 1 | 0 | |
| -1 | -k' | -1 | -k' | |
| 3K' | ∞ | 1/k | ∞ | -1/k |
| ∞ | ik'/k | ∞ | -ik'/k | |
| ∞ | 0 | ∞ | 0 |
特別な場合(k=0, 1)
k = 0 のとき、 sn(u, 0) = sin u cn(u, 0) = cos u dn(u, 0) = 1 k = 1 のとき、 sn(u, 0) = tanh u cn(u, 0) = 1 / cosh u dn(u, 0) = 1 / cosh u
sc, dc など
sn = sinφ(u) cn = cosφ(u) dn = √(1 - k^2 sn^2) に加え、 ns = 1 / sn nc = 1 / cn nd = 1 / dn sc = sn / cn cs = cn / sn cd = cn / dn dc = dn / cn ds = dn / sn sd = sn / dn あわせて12個の楕円関数を定義する。 ↑ 要するに、1文字目が零点、2文字目が極の分布を表していて、 s … 2m K + 2n i K' c … (2m+1)K + 2n i K' d … (2m+1)K + (2n+1) i K' n … 2m K + (2n+1) i K'
加法定理
denom = 1 - k^2 sn^2(u) sn^2(v) とおくと、
sn(u + v) = sn(u) cn(v) dn(v) + cn(u) dn(u) sn(v)
-------------------------------------
denom
cn(u + v) = cn(u) cn(v) - sn(u) dn(u) sn(v) dn(v)
-------------------------------------
denom
dn(u + v) = dn(u) dn(v) - sn(u) cn(u) sn(v) cn(v)
-------------------------------------
denom
虚数
sn(iu, k) = i sn' / cn' = i sc(u, k') cn(iu, k) = 1 / cn' = nc(u, k') dn(iu, k) = dn' / cn' = dc(u, k')
シフト
sn(u + K) = cn(u) / dn(u) = cd cn(u + K) = -k' sn(u) / dn(u) = -k' sd dn(u + K) = k' 1 / dn(u) = k' nd sn(u + iK') = (1/k) 1 / sn(u) = (1/k) ns cn(u + iK') = -(1/k) dn(u) / sn(u) = -i(1/k) ds dn(u + iK') = -i cn(u) / sn(u) = -i cs
k > 1 の場合への拡張
sn(u, 1/k) = k sn(u/k, k) cn(u, 1/k) = dn(u/k, k) dn(u, 1/k) = cn(u/k, k)
複素数
定義域が複素数、すなわち sn(u + iv, k) (u, v∈R) の場合。
sn = sn(u, k), sn' = sn(v, k')
cn = cn(u, k), cn' = cn(v, k')
dn = dn(u, k), dn' = dn(v, k')
と置くと、
加法定理および虚数の場合の公式から
denom = cn'^2 + k^2 sn^2 sn'^2
= 1 - dn^2 sn'^2
sn(u + iv, k) = sn dn' + i cn dn sn' cn'
------------------------
denom
cn(u + iv, k) = cn cn' - i sn dn sn' dn'
------------------------
denom
dn(u + iv, k) = dn cn' dn' - i k^2 sn cn sn'
----------------------------
denom
倍周期・半周期公式
加法定理より、
倍周期公式
denom = 1 - k^2 sn^4(u)
sn(2u) = 2 sn(u) cn(u) dn(u)
-------------------
denom
cn(2u) = 1 - 2 sn^2(u) + k^2 sn^4(u)
---------------------------
denom
cn(2u) = 1 - 2 k^2 sn^2(u) + k^2 sn^4(u)
-------------------------------
denom
半周期公式
sn^2(u/2) = 1 - cn(u)
---------
1 + dn(u)
cd^2(u/2) = dn(u) + cn(u)
-------------
1 + dn(u)
cd^2(u/2) = dn(u) + cn(u)
-------------
1 + cn(u)
u = K/2 のときの値
sn(K/2) = 1 / √(1 + k')
cn(K/2) = √(k' / (1 + k'))
dn(K/2) = √(k')
微分
(d/du)sn = cn dn (d/du)cn = - sn dn (d/du)dn = -k^2 sn cn
メモ(theta 関数)
・テータ関数
以下の4つの関数を、Jacobi のテータ関数(Jacobian theta function)という。
θ1(z, q) = Σ_-∞^∞ (-1)^(n - 1/2) q^((n+1/2)^2) exp((2n + 1) i z)
θ2(z, q) = Σ_-∞^∞ q^((n+1/2)^2) exp((2n + 1) i z)
θ3(z, q) = Σ_-∞^∞ q^(n^2) exp(2n i z)
θ4(z, q) = Σ_-∞^∞ (-1)^n q^(n^2) exp(2n i z)
θの異字体(LaTeX で言う所の \vartheta)を使う方が一般的。
写植の都合で、θあるいはΘを使うこともあり。
ここでは、θで表記。
q をθ関数のノーム(nome、州という意味の単語)という
準二重周期関数を持つ。
θ1(z + π) = -θ1(z)
θ2(z + π) = -θ2(z)
θ3(z + π) = θ3(z)
θ4(z + π) = θ4(z)
θ1(z + τπ) = -N θ1(z)
θ2(z + τπ) = N θ2(z)
θ3(z + τπ) = N θ3(z)
θ4(z + τπ) = -N θ4(z)
q = exp(iπτ)
N = q^-1 exp(-2 i z)
・楕円関数との関係
Jacobi の楕円関数 sn, cn, dn との間に、
θ3 θ1(u / θ3^2, q)
sn(u, k) = ---------------------
θ4 θ4(u / θ3^2, q)
θ4 θ2(u / θ3^2, q)
cn(u, k) = ---------------------
θ2 θ4(u / θ3^2, q)
θ4 θ3(u / θ3^2, q)
dn(u, k) = ---------------------
θ3 θ4(u / θ3^2, q)
(ただし、θi = θi(0) (i = 1~4))
q = exp(-π K'(k) / K(k))
という関係あり。