「フーリエ級数展開」では、
周期性を持つ関数はフーリエ級数に展開出来るという話をしてきました。
ここでは、非周期関数を、「関数の周期TをT→∞としたものである」とみなすことで、
フーリエ級数展開を非周期関数にも適用することを考えてみます。
まず、ω=をいう変数を定義します。
変数ωは、フーリエ級数中ではsinωt, cosωt, expiωtというように、正弦波中で変数tに掛かるため、角周波数と呼ばれます。
角周波数ωは、T→∞としたとき、実数になります。
また、Δω=ω/n=と置き、
フーリエ級数展開の式を以下のように書き換えます。
ここで、F(ω) = と置き、T→∞で極限をとることで、以下の式が得られます。
F
(ω
) =
∫ f
(t
)exp(-iωt
)dt =
∫ f
(t
)exp(-iωt
)dt
f(t) =
F
(ω
)exp( iωt
)Δω =
∫
F
(ω
)exp(iωt
)dω
X
(f
) =
∫ f
(t
)exp(-i2πft
)dt
x(t) =
∫ X
(f
)exp(i2πft
)df
(周波数のfと混同しないように、関数をxで表しています。)
このようにして得られた、連続関数→連続関数の変換をフーリエ変換と呼びます。
f(t)からF(ω)を得る変換を順変換(単に“変換”ということも)、
F(ω)からf(t)に戻す変換を逆変換と呼びます。
式から見て取れる通り、フーリエ変換は指数関数の中の符号と定数倍を除いて、順変換と逆変換の式がまったく同じになります。
フーリエ変換の結果得られた関数F(ω)(またはX(f))を周波数領域表現と呼びます。
これに対して、元々の関数f(t)を時間領域表現と呼んだりします。
表記法としては、
時間領域表現にはアルファベットの小文字、
周波数領域表現には大文字を使用することが多いです。
その他にも、
周波数領域表現にはアルファベットの上に^(ハット記号)を付けて表す記法もあります。
また、関数f(t)をフーリエ変換したものであることを明示するために、
フーリエ変換をℱ[f(t)](ω)というように表す場合もあります(フォントの都合で少しわかりづらいですが、筆記体のFです)。
同様に、フーリエ逆変換はℱ�|1[F(ω)](t)と表します。
フーリエ変換は以下のような性質を持っています。
ℱ[
a f(t)
+
b g(t)]
(ω)
=
a
ℱ[
f(t)](ω)
+
b
ℱ[
g(t)](ω)
=
[
f
(t
)exp(-iωt
)]
-
∫
f
(t
)exp(-iωt
)dt
=
iω
ℱ[
f(t)](ω)
ちなみに、3行目から4行目への変換ですが、
第1項目が消えています。
これは、
通常の関数の意味では、フーリエ変換が収束するためには
f(t)exp(-iωt) が ±∞ で 0 に収束する必要があるので、第1項は 0 になるものとして消しています。
ただし、これはあくまで、微分のフーリエ変換
ℱ[f(t)](ω)
が収束するときにのみ言えることで、
収束の可否については別途調べる必要があります。
=
[∫
f
(τ
)dτ
∫exp(-iωτ
)dτ
]
-
∫
f
(t
)∫exp(-iωτ
)dτ
dt
ℱ[
f(t±T)]
(ω)
=
exp(±iTω
)∫
f
(t
)exp(-iωt
)dt
=
exp(±iTω)ℱ[
f(t)](ω)
関数の積のフーリエ変換
ℱ[
f(t)
×
g(t)](ω)
を直接考えるよりも、
関数f(t), g(t)に対して、
ℱ[
h(t)](ω)
=
ℱ[
f(t)](ω)
×
ℱ[
g(t)](ω)
となるような関数h(t)を探す方が簡単なので、
先にこちらについて説明します。
ℱ[
f(t)]
(ω)
×
ℱ[
g(t)](ω)
はフーリエ変換の定義から以下のように表すことができます。
ℱ[
f(t)]
(ω)
×
ℱ[
g(t)](ω)
=
∫
f
(t
)exp(-iωt
)dt
∫
g
(u
)exp(-iωu
)du
=
∫∫
f
(t
)
g
(u
)exp(-iω
(t+u
))dt
du
ここで、τ=t, υ=t+uと置いて変数変換をすると、
u = υ-τ, dtdu = dτdυなので、
上式は以下のように書き換えることができます。
∫
∫
f
(τ
)
g
(υ-τ
)exp(-iω
(υ
))dτ
dυ
=
∫(∫
f
(τ
)
g
(υ-τ
)dτ
)exp(-iωυ
)dυ
h(t) =
∫
f(τ)
g(t-τ)dτ
と置くと、
この式はℱ[h(t)](ω)となります。
この関数hをfとgの「畳込み積」と呼び、f*gと表します。
ℱ[
f*g(t)]
(ω)
=
ℱ[
f(t)](ω)
×
ℱ[
g(t)](ω)
また、フーリエ変換と逆変換の対称性から、以下の式も成り立ちます。
ℱ[
f(t)
×
g(t)]
(ω)
=
ℱ[
f(t)]
*
ℱ[
g(t)](ω)
前節で説明したとおり、
2つの関数を掛け合わせたものをフーリエ変換すると、畳込み積(convolution product)という特殊な演算が出てきます。
畳込み積は単に畳込み(convolution)と呼ぶこともあります。
改めて、fとgの畳込み積f*gの定義式を書くと以下のようになります。
畳込み積は積のフーリエ変換結果として出てくる演算として定義しました。
では、この演算自体にはどういった意味合いがあるのかという疑問に思う方もいるかと思います。
そこで、畳込み積自体の意味について、具体例を挙げて説明していきます。
簡単な例として、電荷分布の作る電場について考えてみます。
(説明を簡単にするため、1次元的な分布を考えます。)
まず、電気量が1である点電荷が、位置x = 0にある場合に生じる電位をφ0(x)とします。
(例えば、3次元の自由空間上に電荷がある場合にはφ0(x) = 。)
次に、複数の点電荷が作る電位について考えます。
電気量qiを持つN個の電荷(i = 0, 1, …, N-1)が、
それぞれ位置xiにあるとき、
これらの電荷が作る電位は以下のようになります。
これは、下図に示すように、電荷の数だけφ0(x)の位置をずらして、
重みqiを掛けた上で重ね合わせたものになっています。
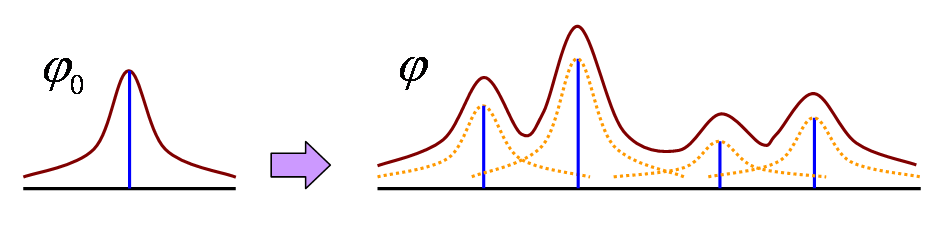 関数の重ね合わせ
関数の重ね合わせ
さらに、電荷が連続的に分布する場合について考えて見ましょう。
電荷密度分布ρ(x)が存在するとき、
ある点ξの近傍にある電荷が作る電位は
dφ = ρ(ξ)φ0(x - ξ)dξ
となります。
これを積分することで電荷全体の作る電位が得られます。
φ
(x
) =
∫
ρ
(ξ
)
φ
0(x - ξ
)dξ
=
ρ*φ
0(x
)すなわち、電位φは、電荷密度分布ρと点電荷の作る電位φ0の畳込み積になります。
この例で示したように、
畳込み積f*gとは、
ある関数gの位置をずらして、
重みとして関数fを掛けた上で重ね合わせたものになります。
「畳込み(convolution)」という言葉は「ずらして重ねあわせる」という意味合いで使われているわけです。
畳み込み積には交換法則および結合法則が成り立ちます。
f*g = g*f
f*(g*h) = (g*f)*h
また、畳込み積の微分・積分は以下のようになります。
∫
(f*g
)
dt
=
(∫f
dt
)*g
=
f*
(∫g
dt
)
さらに、δ関数に対して以下の式が成り立ちます。
{δ(t ± T)}*{f(t)}
=
f(t ± T)
フーリエ変換の性質
|
微分
|
ℱ[
f (t )]
(ω )
=
iω
ℱ[
f (t )](ω )
|
|
積分
|
ℱ[
∫
f (t )dt
]
(ω )
=
ℱ[
f (t )](ω )
|
|
時間シフト
|
ℱ[
f(t±T)]
(ω)
=
exp(±iTω)ℱ[
f(t)](ω)
|
|
積、畳込み積
|
ℱ[
f(t)
×
g(t)]
(ω)
=
ℱ[
f(t)]
*
ℱ[
g(t)](ω)
ℱ[
f
*
g(t)]
(ω)
=
ℱ[
f(t)](ω)
×
ℱ[
g(t)](ω)
|
定数の 1/2π、普通は逆変換側に付けるけど、他にいろんな流儀あり。
順変換側に付けたり、
両方に1/√2πを付けたりとか。
例が欲しいかも。
δ関数、sinc関数、e^(-x^2)とか。
窓掛け
「非周期関数 = 周期∞の関数」
でも、実用上は無限長の区間で信号を測定するのは困難。
↓
信号の一部分だけ切り出してフーリエ変換する。
(窓掛け)
リプル防止のために、切り出す際、窓関数をかける。

