概要

ここでは、ディジタルフィルタの設計手法などについて説明していきます。 （筆者の専門の関係で、音声フィルタを前提とした1次元線形フィルタを中心に説明します。） ディジタル信号処理の知識が必須ですので、 先に「信号処理」を通読しておいてください。

ディジタルフィルタとは

ディジタルフィルタとは、 ディジタル電子計算機などを用いて、 ディジタル信号の特性を変化させるようなもののことを言います。 例えば、信号に混入したノイズを低減させたり、 特定の周波数の信号だけを取り出したりすることが出来ます。

より具体的な例を挙げると、入出力となる信号の種類として、 画像や音声などがあります。 画像の場合、例えば、 「ぼかし」「輪郭強調」などのフィルタがあります。 また、音声の場合には、 「低音の強調」「エコー・リバーブ」などのフィルタがあります。 下図に、画像に「ぼかし」「輪郭強調」フィルタを掛けた例を示します。

ディジタル信号処理おさらい

ディジタルフィルタの話に入る前に、 軽く「信号処理」のおさらいをしておきましょう。

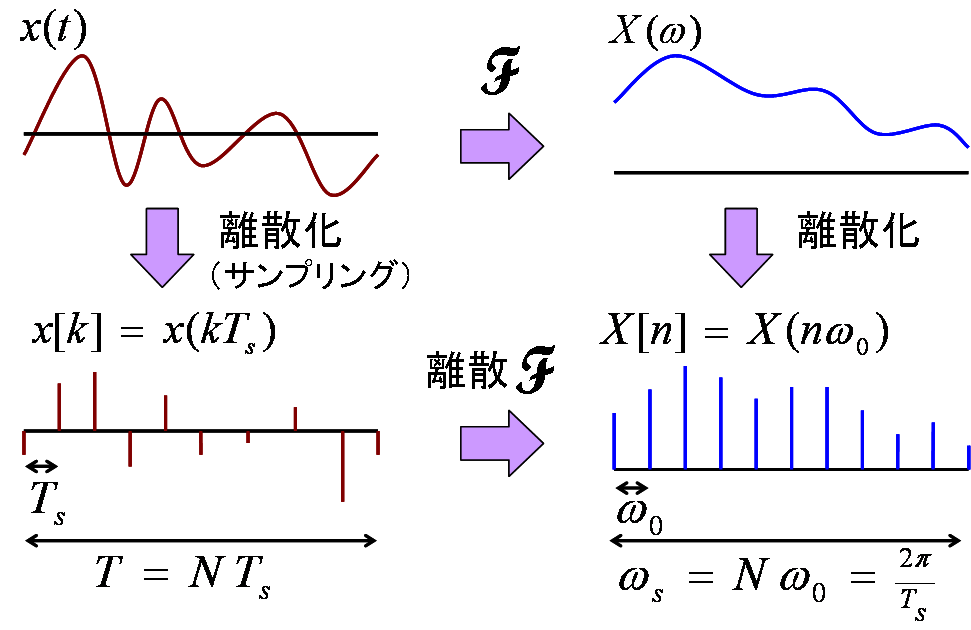
連続信号と離散信号の関係
周波数特性
サンプル

ディジタル信号処理では、過去の信号値を記憶しておいて使う
x[k-1] ＝ D x[k]
等と書く。
D … 遅延

現在の時刻を k としたとき、
x[k-N] ＝ D^n x[k] を「N サンプル前の値」という。

執筆予定

電子計算機などを使って信号処理
↓
離散信号
↓
差分方程式

電子計算機上では、いろんなフィルタを簡単に実現可能。
フィルタの特性を容易に計算できる線形フィルタがよく使われる。
線形フィルタ ＝ 線形差分方程式で表すことの出来るフィルタ。

・線形フィルタ ＝ 線形差分方程式
記憶素子(遅延)と加算器・乗算器があれば実現可能。
差分方程式→ブロック図の例を挙げて説明。

大きく分けて
- 線形フィルタ
  - FIR
  - IIR
- 非線形フィルタ
それぞれの長所と短所を。


Z変換の z－1 は遅延を表す。
伝達関数が z－1 の整式のとき、ループ（再帰）のないフィルタで実現可能。 → FIR
伝達関数が z－1 の有理式のとき、再帰構造が必要。 → IIR


サンプルプログラムも出す？