チェビシェフ有理関数
「ヤコビの楕円関数」cd(x, k) を用いて、 以下のように定義される関数をチェビシェフ有理関数(elliptic rational function)という。
| n K1 |
| K |
k は、
= n を満たすように選ぶ(k' = √)。
ただし、K(k) は第1種完全楕円積分である。K K1' K1 K'
-
チェビシェフ多項式を有理式に拡張したようなもの。
-
k1→0のとき、「チェビシェフ多項式」に。
-
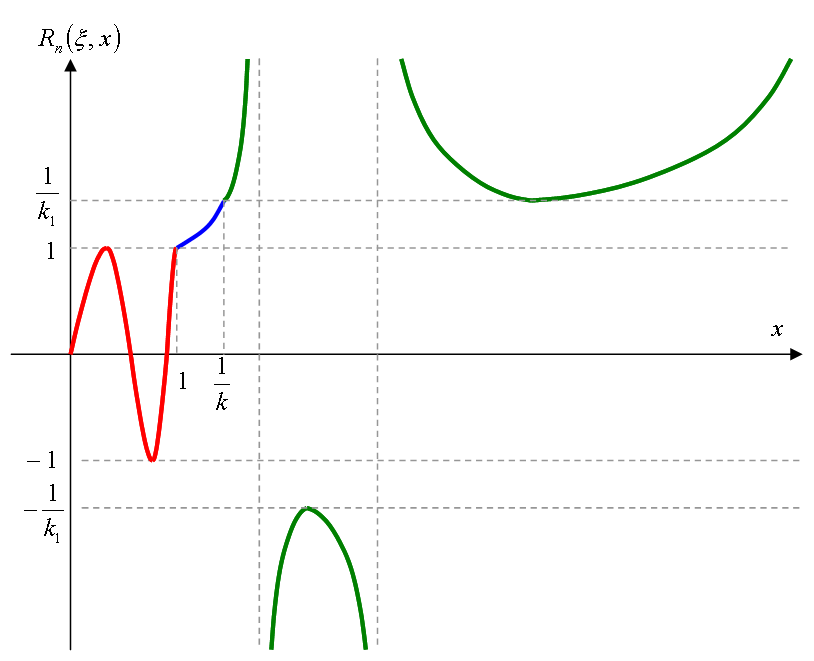
区間[0, 1]で|Rn, k1(x)| < 1
-
区間[1, 1/k1]で単調増加
-
区間[1/k1, ∞]で|Rn, k1(x)| > 1/k1
数値計算上、k は k = q-1( exp ( -
| π K1 |
| n K1' |
)) で求める。 (q(k) は Jacobi のテータ関数のノーム。)
執筆予定
ヤコビの楕円関数の詳細は 「ヤコビの楕円関数」 参照。
関数のグラフ。 ↑の導出の過程。 零点と極 → 有理式で表す。
メモ
基本概念
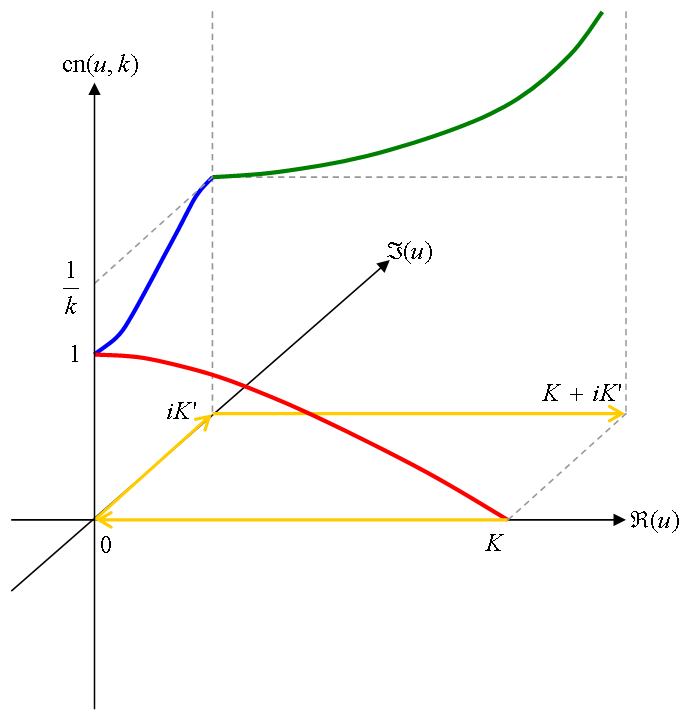
複素平面状に以下のような経路 C = C1 + C2 + C3 を考える。
-
まず、実軸上をK→0と進む(C1)。
-
次に、虚軸上を0→i K'と進む(C2)。
-
最後に、Im(u) = i K'上をi K'→K + i K'と進む(C3)。
経路 C 上での cd(u, k) の値の変化の仕方を表1に、値を3次元的にグラフ化したものを図1に示す。 図1中では、 経路 C をオレンジ色、 C1 上での値を赤色、 C2 上での値を青色、 C3 上での値を緑色の線で表す。
| 経路 | 式変形 | 値の変化の仕方 | ||||
|---|---|---|---|---|---|---|
| C1(K→0) | cd(K - u, k) = sn(u, k) | 0→1の間で単調増加。 | ||||
| C2(0→i K') |
cd(i u, k)
=
|
1→
|
||||
| C3(i K'→K + i K') |
cd(u + i K', k)
=
|
|
cd(u, k) は C 上で単調増加 → cd の逆関数 cd-1(x, k) の実軸上での値は経路 C に。
次に、経路 C に定数
を掛けた経路
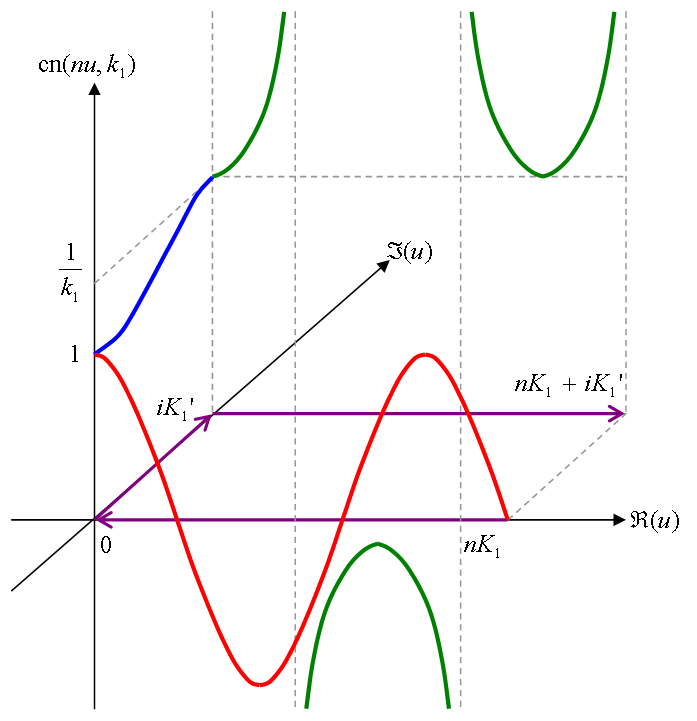
D = D1 + D2 + D3
を考える。n K1 K
-
D1 =
C1… 実軸上をn K1→0と進む。n K1 K -
D2 =
C2… 実軸上を0→i K1'と進む。 (n K1 K
= K1')n K1 K' K -
D3 =
C3…Im(u) = i K1'上をi K1'→n K1 + i K1'と進む。n K1 K
この経路 D 上での cd(u, k1) の値を3次元的にグラフ化したものを図2に示す。 図2中では、 経路 C を紫色、 C1 上での値を赤色、 C2 上での値を青色、 C3 上での値を緑色の線で表す。
「
実軸 [0, ∞] →
(cd-1(x, k))→
経路 C →
(
を掛ける)→
経路 D →
(cd(u, k1))→
Rn, k1(x)」
となるので、チェビシェフ有理関数 Rn, k1(x) のグラフは図3のようになる。n K1 K
零点/極
Rn, k1(x) は n 個の零点と極で表される有理式となる。 まず、Rn, k1(x) の零点/極を求める。 cd(u, k) の零点は
なので、 Rn, k1(x) の零点は、
| n K1 |
| K |
したがって、
K,
k
)
=
sn(2m + 1 n
K,
k
)n - 2m - 1 n
なので、 Rn, k1(x) の極は、
| n K1 |
| K |
したがって、
K + i K',
k
)
=
2m + 1 n 1
k
sn(
K,
k
)n - 2m - 1 n
| n - 2m - 1 |
| n |
| (n - 1) / 2 |
| ∏ |
| m = 0 |
| k2 ωm, n2 - 1 |
| 1 - ωm, n2 |
| x2 - ωm, n2 |
| k2 ωm, n2 x2 - 1 |
| n / 2 |
| ∏ |
| m = 0 |
| k2 ωm, n2 - 1 |
| 1 - ωm, n2 |
| x2 - ωm, n2 |
| k2 ωm, n2 x2 - 1 |