チェビシェフ有理関数

「ヤコビの楕円関数」cd(x, k) を用いて、 以下のように定義される関数をチェビシェフ有理関数（elliptic rational function）という。

k は、

K K1'

K1 K'

＝ n を満たすように選ぶ（k' ＝ √1 － k²）。 ただし、K(k) は第1種完全楕円積分である。

• チェビシェフ多項式を有理式に拡張したようなもの。

• k₁→0のとき、「チェビシェフ多項式」に。

• 区間[0, 1]で|R_{n, k1}(x)| ＜ 1

• 区間[1, 1/k₁]で単調増加

• 区間[1/k₁, ∞]で|R_{n, k1}(x)| ＞ 1/k₁

数値計算上、k は k ＝ q^－1( exp ( －

π K1

n K1'

)) で求める。 （q(k) は Jacobi のテータ関数のノーム。）

執筆予定

ヤコビの楕円関数の詳細は 「ヤコビの楕円関数」 参照。

関数のグラフ。
↑の導出の過程。
零点と極 → 有理式で表す。

メモ

基本概念

複素平面状に以下のような経路 C ＝ C₁ ＋ C₂ ＋ C₃ を考える。

• まず、実軸上をK→0と進む（C₁）。

• 次に、虚軸上を0→i K'と進む（C₂）。

• 最後に、Im(u) ＝ i K'上をi K'→K ＋ i K'と進む（C₃）。

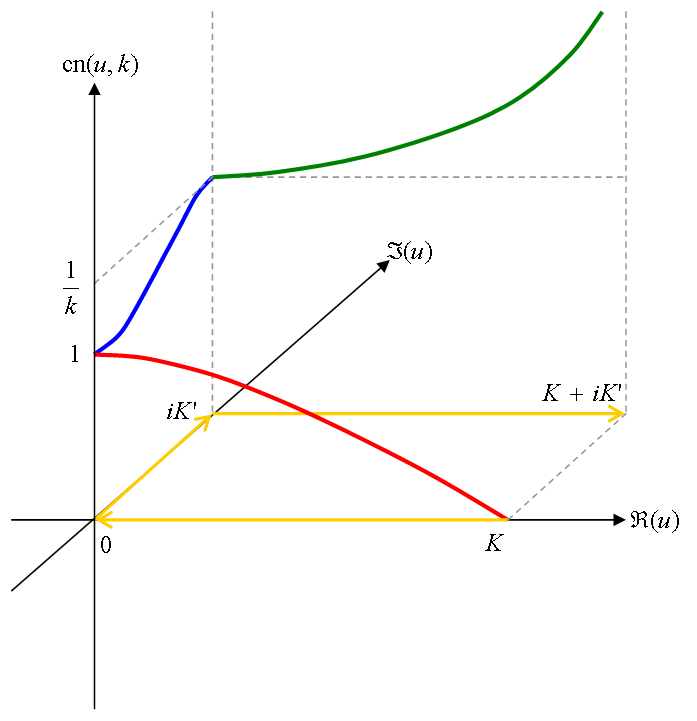
経路 C 上での cd(u, k) の値の変化の仕方を表1に、値を3次元的にグラフ化したものを図1に示す。 図1中では、 経路 C をオレンジ色、 C₁ 上での値を赤色、 C₂ 上での値を青色、 C₃ 上での値を緑色の線で表す。

cn(u, k)の値の変化の仕方

経路	式変形	値の変化の仕方
C1（K→0）	cd(K － u, k) ＝ sn(u, k)	0→1の間で単調増加。
C2（0→i K'）	cd(i u, k) ＝ 1 dn(u, k')	1→ 1 k の間で単調増加。
C3（i K'→K ＋ i K'）	cd(u ＋ i K', k) ＝ 1 k cd(u, k)	1 k →∞の間で単調増加。

cd(u, k) は C 上で単調増加 → cd の逆関数 cd^－1(x, k) の実軸上での値は経路 C に。

次に、経路 C に定数

n K1

K

を掛けた経路 D ＝ D₁ ＋ D₂ ＋ D₃ を考える。

• D₁ ＝

  n K1

  K

  C₁… 実軸上をn K₁→0と進む。

• D₂ ＝

  n K1

  K

  C₂… 実軸上を0→i K₁'と進む。 （

  n K1 K'

  K

  ＝ K₁'）

• D₃ ＝

  n K1

  K

  C₃…Im(u) ＝ i K₁'上をi K₁'→n K₁ ＋ i K₁'と進む。

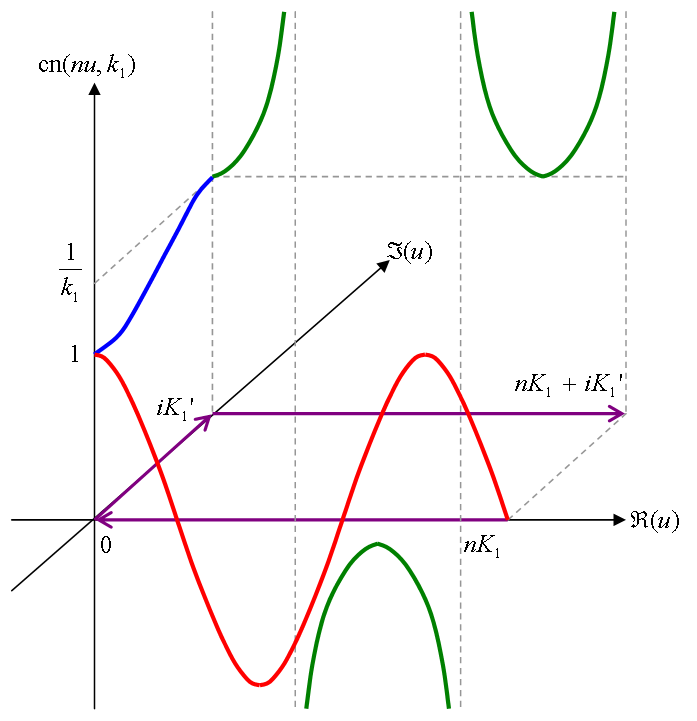
この経路 D 上での cd(u, k₁) の値を3次元的にグラフ化したものを図2に示す。 図2中では、 経路 C を紫色、 C₁ 上での値を赤色、 C₂ 上での値を青色、 C₃ 上での値を緑色の線で表す。

「 実軸 [0, ∞] → （cd^－1(x, k)）→ 経路 C → （

n K1

K

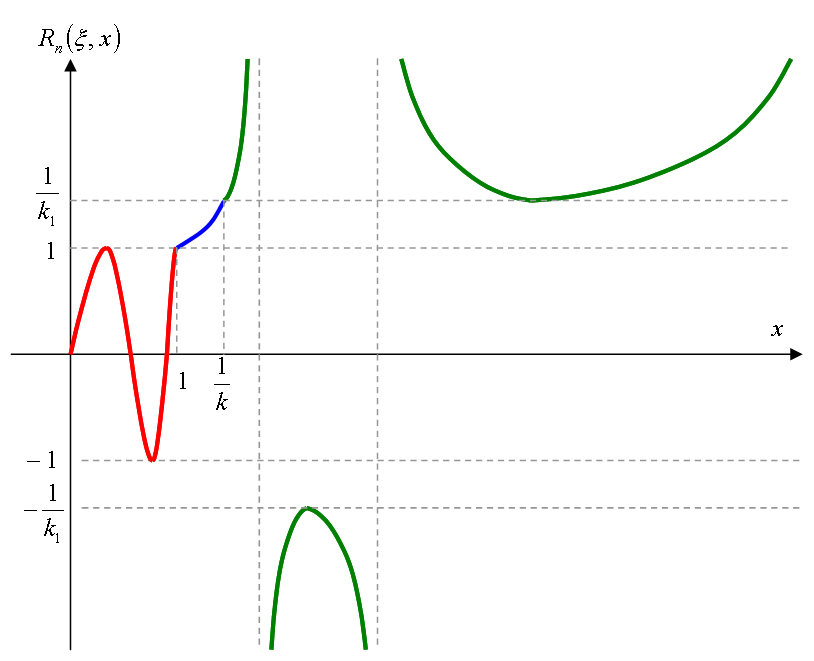
を掛ける）→ 経路 D → （cd(u, k₁)）→ R_{n, k1}(x)」 となるので、チェビシェフ有理関数 R_{n, k1}(x) のグラフは図3のようになる。

零点/極

R_{n, k1}(x) は n 個の零点と極で表される有理式となる。 まず、R_{n, k1}(x) の零点/極を求める。 cd(u, k) の零点は

なので、 R_{n, k1}(x) の零点は、

したがって、

同様に、cd(u, k) の極は

なので、 R_{n, k1}(x) の極は、

したがって、

と置くと、 sn の性質から、 ω_{m, n} ＝ －ω_{n － m － 1, n} となる。 R_{n, k1}(x)は、