分母・分子がともに2次のIIRフィルタを双2次フィルタと呼びます。
双2次フィルタは、以下のような理由から、非常によく利用されています。
以下のような LCR 回路でローパスフィルタが作れます。
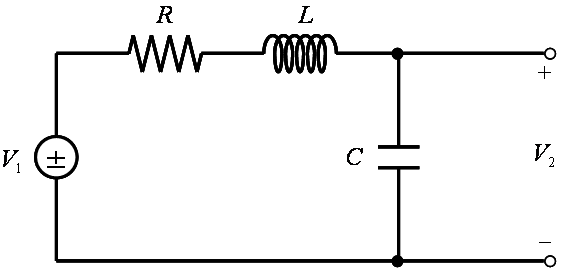 LCR 回路の例
LCR 回路の例
この回路の伝達特性 T(s) は、
T
(s
) =
=
=
| 1 / LC |
| s2 + (R / L) s + 1 / LC |
となります。
ここで、
ω0 = √
(無損失(R = 0)時の共振周波数)、
Q = ω0
= √
(クオリティファクタ(LCR 回路でコイルの損失率を表すパラメータ))
と置くと、
と表すことができます。
この伝達関数の周波数特性は、
ω0 を境にして減衰を始めるローパス特性になっています。
すなわち、このような RCL 回路を用いて、ローパスフィルタを作ることが出来ます。
ちなみに、クオリティファクタ Q を変えると、カットオフ特性のなだらかさなどが変化します。
ここではローパスフィルタを例に挙げましたが、
RCL の配置をいろいろと変えることで、さまざまな特性を作ることができます。
伝達関数の分母・分子ともに2次のフィルタを双2次フィルタ(biquadratic filter、あるいは biquad filter)といいます。
(余談ですが、quad- という接頭語は“4”という意味を表します。
quadratic は“四角形の”という意味合いから“2次元の”という意味で使われる言葉です。
ついでに、bi- は“2”を表す接頭語です。
biquadratic は文字通り解釈すると、“2つの2次元”なわけですが、“4次元の”という意味と、“分母・分子ともに2次元”という意味で使われることがあります。
4(quad)なのに2次、
2×4(biquad)でもやっぱり2次だったり。)
先ほど示したように、RCL 回路を用いてアナログの双2次フィルタを作ることができます。
分母・分子ともに2次という制限の元でも結構いろんなことができます(図2)。
また、双2次フィルタの組み合わせ(直列に繋ぐ)によって、より複雑な特性を作り出すことも出来ます。
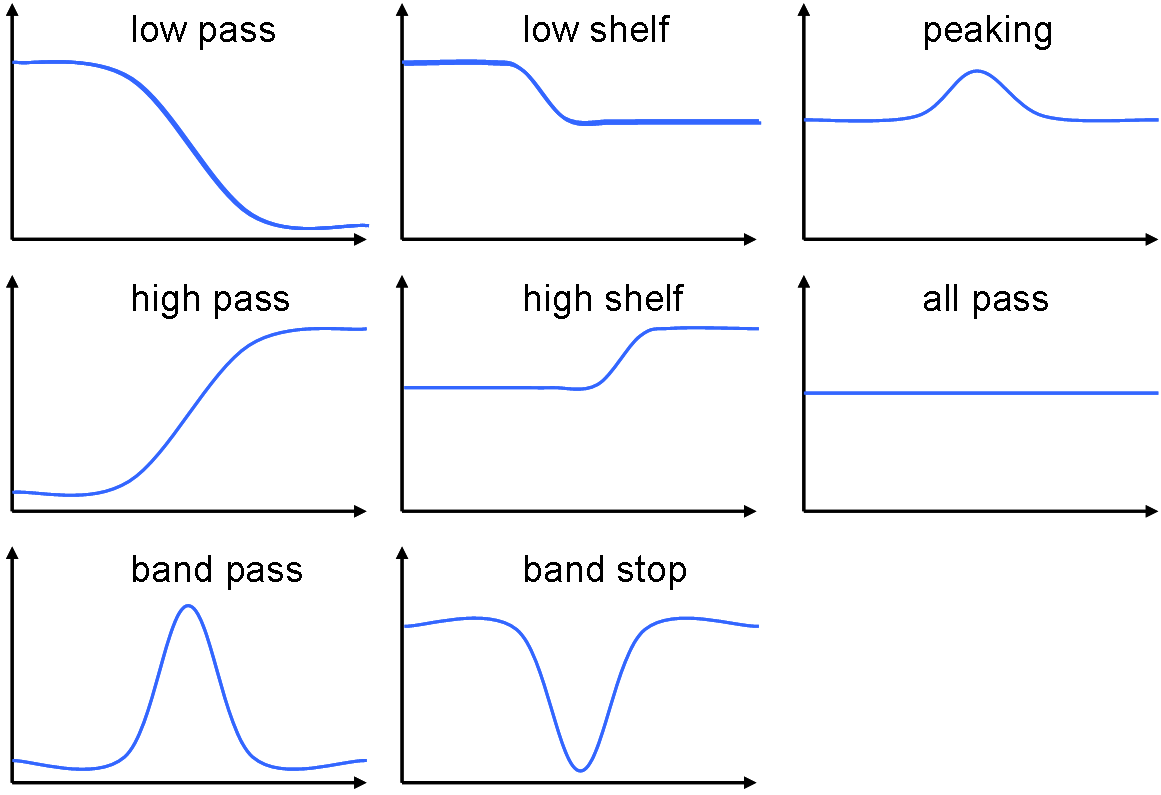 双2次元フィルタの特性いろいろ
双2次元フィルタの特性いろいろ
フィルタ設計が容易であることや、設計手法が確立されたものであることなどから、
双2次フィルタは非常によく利用されています。
Robert Bristow-Johnson という方が、
ネット上で(オーディオ用に)双2次フィルタの設計時に使う公式をまとめたものを公開しています
(通称、RBJ Audio-EQ-Cookbook、参考 URL: http://www.harmony-central.com/Computer/Programming/Audio-EQ-Cookbook.txt)。
以下、この RBJ Cookbook の内容について簡単に説明します(和訳しただけの部分も多いですが)。
設計手法概要
双2次フィルタの設計では、
まず、アナログの双2次伝達関数を作ります。
このとき、フィルタの特性周波数を 1 として伝達関数を作ります。
そして、「周波数変換」で説明したような手法を用いて、周波数変換およびアナログ→ディジタル変換を行います。
双1次変換を用いてアナログ→ディジタル変換を行うと、
フィルタの次数は変わらないので、ディジタルの双2次フィルタを作ることができます。
双2次フィルタを設計する際には、以下のようなパラメータを用います。
-
Fs… ディジタル信号のサンプリング周波数。
-
f0… 特性周波数。要するに、ローパスフィルタならカットオフ周波数、ピーキングフィルタなら中心周波数。
-
gain… ピーキングフィルタやシェルフフィルタの利得[dB]。
-
Q… RCL 回路で説明したクオリティファクタに相当するパラメータ。ローパス・ハイパスフィルタのカットオフ特性や、ピーキングフィルタのピークの鋭さが変わる。
Q に関しては、ピーキングフィルタではピークの幅 BW を、シェルフフィルタではシェルフスロープに関するパラメータ S, a を与えて Q を計算することも多いです。
また、中間的なパラメータとして、以下のようなものを用います。
以下のような式を用いると、周波数変換と双1次変換を同時に行うことができます。
ただし、ω0 は特性周波数 f0を正規化した角周波数です。
tan およびその2乗は、
sin ω0 , cos ω0 を使って書き換えることができるので、
中間パラメータとして sin ω0 , cos ω0 が頻繁に出てくることになります。
以下、具体的な双2次フィルタの話になりますが、
元となるアナログ伝達関数 H(s) と、
ディジタルフィルタの係数 a0 , a1 , a2 , b0 , b1 , b2 のみを示します。
係数の意味は以下の通りです。
H
(z
) =
| b0 + b1 z-1 + b2 z-2 |
| a0 + a1 z-1 + a2 z-2 |
ちなみに、
次節以降で結果だけ示す伝達関数の導出方法ですが、
例えばローパスフィルタなら、
f(0)= 1, f'(0)= 0, f(∞)= 0, f'(∞)= 1
というような条件から係数を計算します。
ローパスフィルタ(low-pass filter)
低域透過フィルタ。
低周波数信号のみを通すフィルタ。
b1
=
1 - cos ω0
a0
=
1 + α
a1
=
-2 cos ω0
a2
=
1 - α
ハイパスフィルタ(high-pass filter)
高域透過フィルタ。
高周波数信号のみを通すフィルタ。
b1
=
-(1 + cos ω0)
a0
=
1 + α
a1
=
-2 cos ω0
a2
=
1 - α
バンドパスフィルタ(band-pass filter)
帯域透過フィルタ。
特定の帯域信号のみを通すフィルタ。
Q によって透過域の利得が変わる(帯域幅一定)ものと、
帯域幅が変わる(利得は Q で一定)のものがある。
帯域幅一定版
b1
=
0
a0
=
1 + α
a1
=
-2 cos ω0
a2
=
1 - α
利得一定版
b0
=
α
b1
=
0
b2
=
-α
a0
=
1 + α
a1
=
-2 cos ω0
a2
=
1 - α
バンドストップフィルタ(band-stop filter)
帯域阻止フィルタ。
特定の帯域信号のみを通さないフィルタ。
ノッチ(notch)フィルタともいう。
b0
=
1
b1
=
-2 cos ω0
b2
=
1
a0
=
1 + α
a1
=
-2 cos ω0
a2
=
1 - α
オールパスフィルタ(all-pass filter)
全域透過フィルタ。
振幅特性はそのまま(全域透過、all-pass)で、
位相特性のみを変化させるフィルタ。
b0
=
1 - α
b1
=
-2 cos ω0
b2
=
1 + α
a0
=
1 + α
a1
=
-2 cos ω0
a2
=
1 - α
ピーキングフィルタ(peaking filter)
振幅特性にピークやディップ(山や谷)を作るフィルタ。
周波数ごとの音量調整に使えるので、音響分野では特によく使われる(いわゆる、イコライザ)。
なので、分野によってはピーキングイコライザ(peaking equalizer)と呼ぶ。
b0
=
1 + α A
b1
=
-2 cos ω0
b2
=
1 - α A
a0
=
1 + α A
a1
=
-2 cos ω0
a2
=
1 - α A
あるいは、
H(s)
=
または
H(s)
=
というように、
A を分母または分子に集中させる場合もある。
(通常、
A が1以上(gain [dB] が正)のとき分母に、
A が1以下(gain [dB] が負)のとき分子に集中させる。)
ローシェルフフィルタ(low-shelf filter, low-shelving filter)
振幅特性の低域に棚状の利得をかける。
ローブースト(low-boost)フィルタともいう。
b0
=
A
((A + 2)
-
(A - 2)cos ω0
+
2 √A α
)
b1
=
-2 A
((A - 2)
-
(A + 2)cos ω0)
b2
=
A
((A + 2)
-
(A - 2)cos ω0
-
2 √A α
)
a0
=
(A + 2)
+
(A - 2)cos ω0
+
2 √A α
a1
=
2
((A - 2)
+
(A + 2)cos ω0)
a2
=
(A + 2)
+
(A - 2)cos ω0
-
2 √A α
ハイシェルフフィルタ(high-shelf filter, high-shelving filter)
振幅特性の高域に棚状の利得をかける。
ハイブースト(high-boost)フィルタともいう。
b0
=
A
((A + 2)
+
(A - 2)cos ω0
+
2 √A α
)
b1
=
2 A
((A - 2)
+
(A + 2)cos ω0)
b2
=
A
((A + 2)
+
(A - 2)cos ω0
-
2 √A α
)
a0
=
(A + 2)
-
(A - 2)cos ω0
+
2 √A α
a1
=
-2
((A - 2)
-
(A + 2)cos ω0)
a2
=
(A + 2)
-
(A - 2)cos ω0
-
2 √A α


