3次元空間中での回転は、回転軸と回転角で表すことができます。
実用上、回転軸
p
=
(
px ,
py ,
pz
)
と回転角
θ
は、以下のような形式に変換して置くことが多いです。
(
cos
,
sin
p
x ,
sin
p
y ,
sin
p
z
)
これを、以下のように表したりもします。
この形式を四元数といいます。
四元数なんていうたいそうな名前が付いているは、
元をただせば数学的な意味があるからなんですが、
四元数の数学的意味は、画像処理・3D CG の分野では大して役に立ちません。
応用上は、元々の数学的な意味を知る必要はあまりなく、
回転軸
p
=
(
px ,
py ,
pz
)
と回転角
θ
の情報を、
4次元の単位ベクトルとして、
(
cos
;
sin
p
)
=
(
cos
,
sin
p
x ,
sin
p
y ,
sin
p
z
)
という形式で持っているものとだけ覚えておけば十分。
まず、3次元空間上の回転を定式化します。
3次元空間上の回転を表すためには、回転軸ベクトル
p
と回転角度 θが必要になります。
回転軸ベクトルの絶対値は意味を持たないので、
|
p
|
=
1
であるものとしてます。
座標ベクトル
u
で表される点 A を、回転軸
p
を中心に角度 θ 回転した点 A' の座標ベクトル
u'
は、以下のような計算で求めることができます。
u'
=
sinθ u
×
p
+
cosθ (
u
−
(
u
⋅
p
)
p
)
+
(
u
⋅
p
)p
=
sinθ u
×
p
+
cosθ
u
+
(
1 − cosθ
)
(
u
⋅
p
)
p
ちなみに、この式の導出の仕方ですが、下図のようになります。
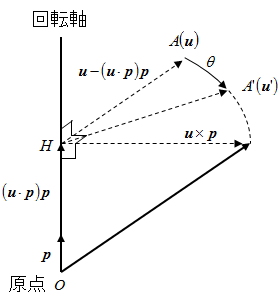3次元ベクトルの回転
原点を O、点 A から回転軸におろした垂線の足を H とすると、
OH
=
(
u
⋅
p
)
p
HA
=
u
−
(
u
⋅
p
)
p
となります。
また
u
×
p
は、
p
および
HA
に垂直で、
絶対値が
|
HA
|
と等しいベクトルになります。
HA'
は、
HA' = cosθ HA + sinθ u×p
=
sinθ u
×
p
+
cosθ
u
+
(
1 − cosθ
)
(
u
⋅
p
)
p
と表すことができるので、先ほど示した式を導き出すことができます。
前節で示した式で3次元空間中の回転が表現できるんですが、
実際には、この式をそのまま使うのではなく、行列演算に変形してから使います。
(行列にすることで、拡大縮小や平行移動などと一緒に、まとめて扱えるため。）
3次元ベクトルの外積計算は以下のように、
p
×
u
=
u
[|
0
|
−pz
|
py
|
|
pz
|
0
|
−px
|
|
−py
|
px
|
0
|
]
行列とベクトルの積としても書き表わせます。
（ただし、ベクトルは横ベクトルを仮定しています。）
また、
(
u
⋅
p
)
p
という部分も、
(
u
⋅
p
)
p
=
u
[|
px2
|
px py
|
pz px
|
|
px py
|
py2
|
py pz
|
|
pz px
|
py pz
|
pz2
|
]
と表せます。
これらを使うと、
先ほどの回転の式は、以下のような行列で表すことができます。
u'
=
sinθ u
×
p
+
cosθ
u
+
(
1 − cosθ
)
(
u
⋅
p
)
p
=
cosθ
u
+
(
1 − cosθ
)
u
[|
px2
|
px py
|
pz px
|
|
px py
|
py2
|
py pz
|
|
pz px
|
py pz
|
pz2
|
]
+
sinθ
u
[|
0
|
−pz
|
py
|
|
pz
|
0
|
−px
|
|
−py
|
px
|
0
|
]
=
u
[|
(
1 − cosθ
)
px2
+
cosθ
|
(
1 − cosθ
)
px py
−
pz
sinθ
|
(
1 − cosθ
)
pz px
+
py
sinθ
|
|
(
1 − cosθ
)
px py
+
pz
sinθ
|
(
1 − cosθ
)
py2
+
cosθ
|
(
1 − cosθ
)
py pz
−
px
sinθ
|
|
(
1 − cosθ
)
pz px
−
py
sinθ
|
(
1 − cosθ
)
py pz
+
px
sinθ
|
(
1 − cosθ
)
pz2
+
cosθ
|
]
ここで話を四元数に戻します。
四元数は、
回転軸
p
=
(
px ,
py ,
pz
)
と回転角
θ
の情報を、以下の形式で保持するものです。
(
cos
;
sin
p
)
=
(
cos
,
sin
p
x ,
sin
p
y ,
sin
p
z
)
ここで、sin や cos を何度も書きたくないので、
以下のように書き表わすことにします。
q
=
(
q
w ,
q
x ,
q
y ,
q
z ,
)
=
(
cos
,
sin
p
x ,
sin
p
y ,
sin
p
z
)
ここで、三角関数の倍角の公式を使うと、以下の等式が導かれます。
（* と † の位置には、x, y, z のいずれかが入ります。）
2
q
*
q
†
=
2
sin2
p
*
p
†
=
(
1 − cosθ
)
p
*
p
†
2
q
w
q
*
=
2
sin
cos
p
*
=
sinθ
p
*
2
q
w2
=
2
cos2
=
1
+
cosθ
これらを、前節で求めた行列に代入すると、
以下の結果が得られます。
u'
=
u
[|
2
(
qx2
+
qw2
)
−
1
|
2
(
qx
qy
−
qz
qw
)
|
2
(
qx
qz
+
qy
qw
)
|
|
2
(
qx
qy
+
qz
qw
)
|
2
(
qy2
+
qw2
)
−
1
|
2
(
qy
qz
−
qx
qw
)
|
|
2
(
qx
qy
−
qy
qw
)
|
2
(
qy
qz
+
qx
qw
)
|
2
(
qz2
+
qw2
)
−
1
|
]
あるいは、
|
q
|
=
1
なことを利用して、以下のようにも書けます。
u'
=
u
[|
1
−
2
(
qy2
+
qz2
)
|
2
(
qx
qy
−
qz
qw
)
|
2
(
qx
qz
+
qy
qw
)
|
|
2
(
qx
qy
+
qz
qw
)
|
1
−
2
(
qz2
+
qx2
)
|
2
(
qy
qz
−
qx
qw
)
|
|
2
(
qx
qy
−
qy
qw
)
|
2
(
qy
qz
+
qx
qw
)
|
1
−
2
(
qx2
+
qy2
)
|
]
ちなみに、こうやって作られた行列は、必ず直交行列になります。
（実際、計算してみてもらうと、各列が正規直行していることがわかります。）
回転しかしていないんだから、長さも角度も変わらない変換（＝ 直交行列による1次変換）になっていないとおかしいはずです。
