概要
「ゲート」で説明しますが、コンピューターの内部では電圧の高低で0, 1 の 2 値で数字を表現します。 一方で、私たち人間は普段、10進数というものを用いて数字を表現しています。 ただし、「普段、10 進数を用いている」と言っても、何気なく使っていて、数字の表現方法を意識することはあまりないと思います。 そこで本章では、2 進数や10 進数など、数字の表現方法について改めて説明していきます。
数字の表し方いろいろ
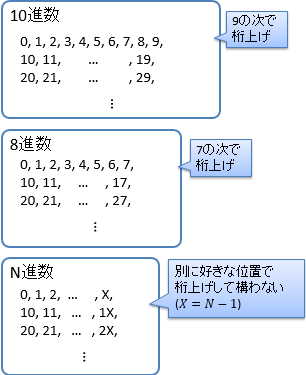
私たちは普段、10進数というものを使っているわけですが、本当のところは別にどんな表し方をしてもかまいません。 0, 1, 2, …, 9という10個の文字を必ずしも使う必要はありません。 図1に示すように、いろいろな表し方があります。 極端な話、利便性を度外視すれば、個数分だけ点や棒を並べるだけでもかまいません。 数が多くなってくるとこれでは不便なので、利便性を考えた結果、0 ~ 9という記号を使うわけです。 ただ、あまり記号を増やしすぎると覚えきれなくなるので、9の次は「桁上げ」というものを使って10と書きます。
ちなみに、図2に示すように、「桁上げ」を使うにしても、いくつで桁上げするかは自由に選べます。 10進数の場合は9の次で桁上げして10になりますが、例えば、7の次で桁上げすれば8進数、1の次なら2進数になります。
また、10進数を使うにしても、0 ~ 9という文字以外のものを使ったってかまいません。 例えば、0 ~ 9の代わりに「あかさたなはまやらわ」を使って、1,980を「か、わらあ」と書いてもいいわけです。 これは少々極端な例ではありますが、とにかく、数字を表す際、何の文字を使うか・桁上げをどうするかなど、いくらでも自由な選択が可能です。
日常で使われる数字
日常で、10進数(decimal number)というものが普及している理由は、おそらく人間の指の本数が左右合わせて10本だからでしょう。 片手じゃなくて両手なのは、片手の5だとちょっと数字として小さすぎるからかもしれません。 人間が瞬時に認識できる/短期的にぱっと暗記できるものの個数は大体7±2個くらいだなんて話もあって、その下限の5だと少し心もとないです。
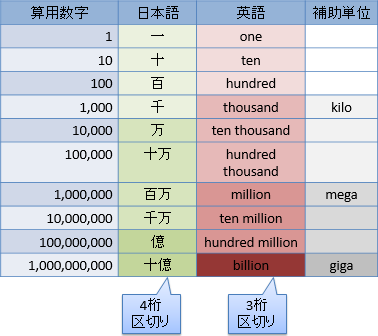
あと、よく考えてみると、図3に示すように、日常的にもう1つ別のn進数が使われています。 算用数字で1, 10, 100, 1000, …と書く分には10進数しか使っていないですが、一、十、百、千、万、…と読み上げると、もう1つ、万進数というものが出てくることに気づきます。 一~千までは10倍ずつですが、万以降は、万、億、兆、京、…と1万倍ずつになります。 英語の場合は万進数ではなく、千進数ですね。thousand, million, billion, trillion, …が1千倍ずつです。 科学で使われる補助単位のkilo, mega, giga, …なども同様に1千倍ずつになっています。
桁上げの数学的表現
最後に、「桁上げ」というものを数学的にどう表すのかと、異なる進数の間での変換について説明します。
10進数で表された数字を一般的に表すと、K 桁の場合には
という数字の並びになります。 この数値を数式として表すと、以下のようになります。
| K−1 |
| ∑ |
| i = 0 |
(∑記号は、数列の和を表します。) 例えば、10進数で1234なら 4 + 3 × 10 + 2 × 102 + 1 × 103 となるわけです。 同様に、N進数の場合は以下のように表すことができます(10のところが N に変わっただけです)。
| K−1 |
| ∑ |
| i = 0 |
この式から、数値をN進数で表現する方法が見えてきます。 数値を N で割って余りを取ると、各桁の数字を得ることができます。
具体例を見てみましょう。上の式を N で割ると以下のようになります。
| K−1 |
| ∑ |
| i = 0 |
これをさらにもう1度割ると、以下のようになります。
| K−1 |
| ∑ |
| i = 0 |
このように、Nで割った余りを取っていくことで、 a0, a1, a2, ... と、各桁の数字を逐次求めることができます。
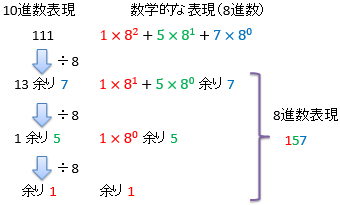
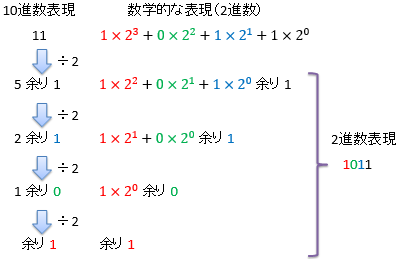
この流れを絵で表してみましょう。 10進数の111を8進数に変換する例を図4に、 10進数の11を2進数に変換する例を図5にしめします。